Monty Hall, who passed away in 2017 was born 100 years ago today: August 25, 1921. He was host of Let's Make a Deal for 30 years. In 2008 I wrote about the "Monty Hall Problem" at The Partial Observer. This is an edited, revised, and shortened version.
Some time ago, I caught some episodes of Breaking the Magician's Code: Magic's Biggest Secrets Finally Revealed, which originally aired in the late 1990's. Yes, several tricks really do depend on "smoke and mirrors." Others exploit lighting and background colors, use hidden compartments, rely on split-second timing, and use sleight-of-hand to "verify" there is nothing fishy with the props and equipment. Other tricks rely on spatial illusions: it doesn't look like any adult can fit into that small container, but, it turns out, a flexible woman really can. Some more extravagant, made-for-television tricks rely on careful camera work, multiple stages, and an audience that is in on the trick, even though no special effects are used.
Being tricked doesn't make us fools. It just means that memories of previous perceptions cause our vision to falsely "connect the dots" when faced with different but similar-looking images.
For another example of seeing an illusion rather than reality, take a look at this image (which I don't have permission to upload here):
http://www.psy.ritsumei.ac.jp/~akitaoka/FraSpr01.gif
Even after being told there is no spiral, only circles, I still perceive a spiral. Yes, looking closely and carefully at it, I do see circles instead, but this information doesn't change my general perception when I'm just glancing at it. My eyes are still fooled even when I know the truth.
(You may view other similarly stunning images here.)
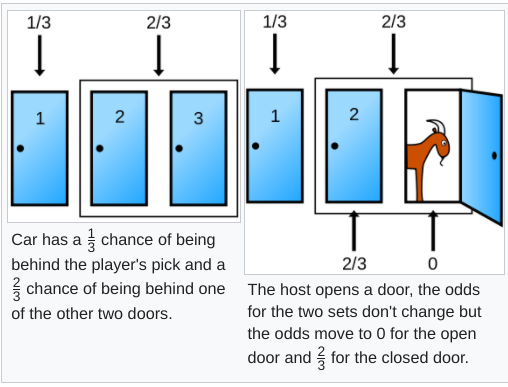
Our eyes can mislead us. More disturbing, however, is how that the mind misleads us. An example of this is the Monty Hall Problem. Hall was the longtime host of Let's Make a Deal, and presented contestants with choices similar to the one described below. The problem goes:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?
Most people, and I was one of them, would use "common-sense" and say there's no reason to switch: the two remaining doors have an equal chance. But Marilyn vos Savant, the high-IQ Parade "Ask Marilyn" columnist, gave an answer that generated thousands of letters in disagreement, including criticism from mathematicians with PhDs. She recommended switching to door #2
Savant was correct. The odds that the car is behind door #1 don't improve after being shown door #3. Door #1 had a one-in-three chance, which means a two-in-three chance that the car's behind door #2 or door #3. There's still a two-thirds chance the car is behind door #2 or door #3, even after #3's is eliminated. Therefore, it is two-thirds likely that the car is behind door #2. That said, all the options had to be shown in pictures for me to understand this (source: Wikipedia).
When the host reveals the goat behind Door 3, he creates the mental illusion that your odds went from one-in-three to one-in-two. But that misunderstands the nature of the new information. The underlying facts didn't change; the odds were one-in-three and remain so, and acting upon the new information and switching to door #2 will increase your odds to two-in-three.
It's tricky to trust even our own senses: "I swear I saw a spiral!" And it's easy to misapply new information: "My odds improved! I'll stick with Door 1!"
And to think how we let equally error-prone individuals exercise authority over us.
James Leroy Wilson writes from Nebraska. Follow him on Facebook and Twitter. If you enjoy his articles, subscribe and exchange value for value. You may contact James for your writing, editing, and research needs: jamesleroywilson-at-gmail.com. Permission to reprint is granted with attribution.